Isserlis' theorem

In probability theory, Isserlis’ theorem or Wick’s theorem is a formula that allows one to compute higher-order moments of the multivariate normal distribution in terms of its covariance matrix.

This theorem is particularly important in particle physics, where it is known as Wick’s theorem after the work of Wick (1950). Other applications include the analysis of portfolio returns,^[1] quantum field theory^[2] and generation of colored noise.^[3]

Theorem statement

If (x₁, …, x_2n) is a zero mean multivariate normal random vector, then

$\begin{align} & \operatorname{E}[\,x_1x_2\cdots x_{2n}\,] = \sum\prod \operatorname{E}[\,x_ix_j\,], \\ & \operatorname{E}[\,x_1x_2\cdots x_{2n-1}\,] = 0, \end{align}$

where the notation ∑ ∏ means summing over all distinct ways of partitioning x₁, …, x_2n into pairs.^[4]. This yields 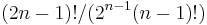$(2n -1)!/(2^{n -1}(n -1)!)$ terms in the sum. For example, for fourth order moments (four variables) there are three terms. For sixth-order moments there are 3 × 5 = 15 terms, and for eighth-order moments there are 3 × 5 × 7 = 105 terms (as you can check in the examples below).

In his original paper, Isserlis (1918) proves this theorem by mathematical induction, generalizing the formula for the fourth-order moments,^[5] which takes appearance

$\operatorname{E}[\,x_1x_2x_3x_4\,] = \operatorname{E}[x_1x_2]\,\operatorname{E}[x_3x_4] %2B \operatorname{E}[x_1x_3]\,\operatorname{E}[x_2x_4] %2B \operatorname{E}[x_1x_4]\,\operatorname{E}[x_2x_3].$

Another example of Isserlis' theorem is:

$\begin{align} & {} E[X_1 X_2 X_3 X_4 X_5 X_6] \\ &{} = E[X_1 X_2 ]E[X_3 X_4 ]E[X_5 X_6 ] %2B E[X_1 X_2 ]E[X_3 X_5 ]E[X_4 X_6] %2B E[X_1 X_2 ]E[X_3 X_6 ]E[X_4 X_5] \\ &{} %2B E[X_1 X_3 ]E[X_2 X_4 ]E[X_5 X_6 ] %2B E[X_1 X_3 ]E[X_2 X_5 ]E[X_4 X_6 ] %2B E[X_1 X_3]E[X_2 X_6]E[X_4 X_5] \\ &%2B E[X_1 X_4]E[X_2 X_3]E[X_5 X_6]%2BE[X_1 X_4]E[X_2 X_5]E[X_3 X_6]%2BE[X_1 X_4]E[X_2 X_6]E[X_3 X_5] \\ & %2B E[X_1 X_5]E[X_2 X_3]E[X_4 X_6]%2BE[X_1 X_5]E[X_2 X_4]E[X_3 X_6]%2BE[X_1 X_5]E[X_2 X_6]E[X_3 X_4] \\ & %2B E[X_1 X_6]E[X_2 X_3]E[X_4 X_5 ] %2B E[X_1 X_6]E[X_2 X_4 ]E[X_3 X_5] %2B E[X_1 X_6]E[X_2 X_5]E[X_3 X_4]. \end{align}$

Bartosch, L. (2001). "Generation of colored noise". International Journal of Modern Physics C 12 (6): 851–855. doi:10.1142/S0129183101002012.
Isserlis, L. (1916). "On Certain Probable Errors and Correlation Coefficients of Multiple Frequency Distributions with Skew Regression". Biometrika 11: 185–190. JSTOR 2331846.
Isserlis, L. (1918). "On a formula for the product-moment coefficient of any order of a normal frequency distribution in any number of variables". Biometrika 12: 134–139. JSTOR 2331932.
Koopmans, Lambert G. (1974). The spectral analysis of time series. San Diego, CA: Academic Press.
Michalowicz, J.V.; Nichols, J.M.; Bucholtz, F.; Olson, C.C. (2009). "An Isserlis’ theorem for mixed Gaussian variables: application to the auto-bispectral density". Journal of Statistical Physics 136 (1): 89–102. doi:10.1007/s10955-009-9768-3.
Perez-Martin, S.; Robledo, L.M. (2007). "Generalized Wick’s theorem for multiquasiparticle overlaps as a limit of Gaudin’s theorem". Physical Review C 76. doi:10.1103/PhysRevC.76.064314.
Repetowicz, Przemysław; Richmond, Peter (2005). "Statistical inference of multivariate distribution parameters for non-Gaussian distributed time series". Acta Physica Polonica B 36 (9): 2785–2796. http://th-www.if.uj.edu.pl/acta/vol36/pdf/v36p2785.pdf.
Wick, G.C. (1950). "The evaluation of the collision matrix". Physical Review 80 (2): 268–272. doi:10.1103/PhysRev.80.268.

Isserlis' theorem

Theorem statement

See also

References